When a charge is kept in the electric field, the Electric Force acts upon it. The Acceleration in the Electric Field Calculator is a tool that will help you to calculate the acceleration caused. Explanation of Acceleration in an Electric Field Formula
Acceleration in Electric Field Calculator
Ckg
V/m
| Parameter | Value |
|---|---|
| Charge (q) | [Calculated Value] C |
| Mass (m) | [Calculated Value] kg |
| Electric Field Strength (E) | [Calculated Value] V/m |
| Acceleration (a) | [Calculated Value] m/s² |
The formula for acceleration in an electric field is used to calculate the acceleration of a charged particle when it is placed in an electric field. This formula takes into account the charge of the particle (\(q\)), the mass of the particle (\(m\)), and the strength of the electric field (\(E\)). The acceleration (\(a\)) of the particle can be calculated using the following formula:
\[a = \frac{F}{m} = \frac{qE}{m}\]
Where:
- \(a\) is the acceleration of the particle.
- \(q\) is the charge of the particle.
- \(m\) is the mass of the particle.
- \(E\) is the electric field.
In this context:
- \(q\) represents the charge of the particle, which can be either positive or negative, and it is measured in coulombs (C).
- \(m\) represents the mass of the particle and is typically measured in kilograms (kg).
- \(E\) represents the strength of the electric field and is measured in volts per meter (V/m).
It’s important to note that in the International System of Units (SI), the elementary charge (\(e\)) is often used as a standard unit for charge, where \(e\) is approximately equal to \(1.6 \times 10^{-19}\) coulombs (C), which is the charge of a single electron. Similarly, the mass of particles is measured in kilograms.
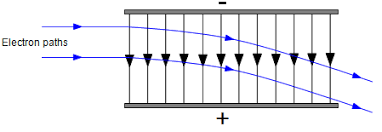
The formula for acceleration in an electric field is derived from Newton’s second law, \(F = ma\), where \(F\) represents the force acting on an object, \(m\) is its mass, and \(a\) is its acceleration. In this case, the force \(F\) is the electrostatic force (\(F = qE\)) due to the interaction between the charge \(q\) and the electric field \(E\). Therefore, combining these two equations gives us the formula for acceleration in an electric field.
This formula is fundamental in understanding the motion of charged particles in electric fields, as it helps predict how they will accelerate or decelerate based on their charge and mass when subjected to an electric field.
Thanks for reading the post Acceleration in the Electric Field Calculator.