Complex Number Calculator is a tool to get the result of arithmetic operations on two complex numbers. You will also get the Magnitude and Phase values after each operation.
What is a Complex Number?
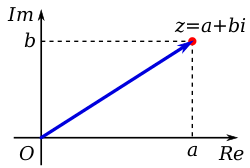
A complex number is a mathematical quantity that comprises both a real part and an imaginary parts. It is expressed in the form “a + bi,” where “a” is the real part, “b” is the imaginary part, and “i” represents the imaginary unit, which is defined as the square root of -1. In this representation, “a” and “b” are real numbers.
What is a Complex Number?
The real part of a complex number contributes to its position on the real number line, while the imaginary part contributes to its position on the imaginary number line. Complex numbers are commonly used to represent quantities that involve both magnitude and phase, making them valuable in various mathematical and scientific applications, including engineering, physics, and signal processing.
Complex numbers can be operated on using mathematical operations such as addition, subtraction, multiplication, and division, just like real numbers. The concept of complex conjugates is also important, where the conjugate of a complex number “a + bi” is “a – bi.”
The complex number plane, also known as the complex plane or Argand diagram, is used to visualize complex numbers. In this plane, the real part corresponds to the horizontal axis, while the imaginary part corresponds to the vertical axis.
In summary, a complex number is a mathematical entity that combines real and imaginary parts to represent quantities involving both magnitude and phase. It plays a crucial role in various mathematical and scientific disciplines, allowing for the representation and manipulation of a wide range of phenomena.
How it Works?
Performing arithmetic operations on complex numbers involves manipulating their real and imaginary parts according to the rules of algebra. For example: Lets us take two complex numbers: “a + bi” and “c + di”:
- Addition: To add two complex numbers “a + bi” and “c + di,” simply add their real parts and imaginary parts separately: Result = (a + c) + (b + d)i
- Subtraction: To subtract the second complex number from the first, subtract their real parts and imaginary parts separately: Result = (a – c) + (b – d)i
- Multiplication: To multiply two complex numbers “a + bi” and “c + di,” use the distributive property and FOIL method: Result = (ac – bd) + (ad + bc)i
- Division: To divide the first complex number by the second, use the concept of complex conjugates to rationalize the denominator: This Result is \[ ((ac + bd) / (c^2 + d^2)) + ((bc – ad) / (c^2 + d^2))i \]
The operations are performed separately for the real and imaginary parts of the complex numbers. Additionally, the complex conjugate of a complex number “a + bi” is “a – bi,” which is often used in division to rationalize the denominator.
Thanks for reading the post Complex Number Calculator.