If you have two vectors and you want to get the cross product of these vector, use the Cross Product Calculator. The cross product of two vectors is a mathematical operation that results in another vector that is perpendicular to both of the original vectors. It’s commonly used in physics and engineering to find the direction of a vector that’s perpendicular to a plane defined by two other vectors. The magnitude of the resulting vector is also related to the original vectors and the sine of the angle between them.
Cross Product of two Vectors
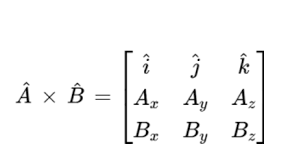
Let’s say you have two vectors, \( \vec{A} \) and \( \vec{B} \), which are represented in three-dimensional space as follows:
\[
\vec{A} = A_x \hat{i} + A_y \hat{j} + A_z \hat{k}
\]
\[
\vec{B} = B_x \hat{i} + B_y \hat{j} + B_z \hat{k}
\]
To calculate the cross product \( \vec{C} \) of vectors \( \vec{A} \) and \( \vec{B} \), you can use the following formula:
\( \vec{C} = \vec{A} \times \vec{B} \)
Here’s how to calculate the components of \( \vec{C} \) using the determinant of a matrix:
\[
\vec{C}_x = (A_y \cdot B_z – A_z \cdot B_y) \hat{i}
\]
\[
\vec{C}_y = (A_z \cdot B_x – A_x \cdot B_z) \hat{j}
\]
\[
\vec{C}_z = (A_x \cdot B_y – A_y \cdot B_x) \hat{k}
\]
So, the cross product \( \vec{C} \) of vectors \( \vec{A} \) and \( \vec{B} \) will be:
\[
\vec{C} = \vec{C}_x \hat{i} + \vec{C}_y \hat{j} + \vec{C}_z \hat{k}
\]
The resulting vector \( \vec{C} \) is orthogonal (perpendicular) to both \( \vec{A} \) and \( \vec{B} \). The magnitude of \( \vec{C} \) is given by:
\[
|\vec{C}| = \sqrt{\vec{C}_x^2 + \vec{C}_y^2 + \vec{C}_z^2}
\]
This method works for three-dimensional vectors. In two dimensions, the cross product is simpler and is equivalent to the scalar value representing the “signed area” of the parallelogram formed by the two vectors.
Keep in mind that the direction of the cross product vector is determined by the right-hand rule: if you curl your right-hand fingers from the direction of vector \( \vec{A} \) to vector \( \vec{B} \), your thumb points in the direction of vector \( \vec{C} \).
Thanks for reading the article Cross Product Calculator.