The Equation of Ellipse Calculator is a tool that can give you the equation of the Ellipse based on the inputs provided.
Ellipse Equation Calculator
To derive the equation of an ellipse, consider its properties and characteristics. The general equation of an ellipse in standard form is given by:
\[
\frac{{(x – h)^2}}{{a^2}} + \frac{{(y – k)^2}}{{b^2}} = 1
\]
Where:
(h, k) are the coordinates of the center of the ellipse.
\(a\) is the length of the semi-major axis (half the length of the longer axis).
\(b\) is the length of the semi-minor axis (half the length of the shorter axis).
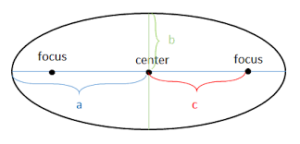
To derive this equation, consider the following properties:
The center of the ellipse is \((h, k)\).
The major axis is the longest diameter of the ellipse, with length \(2a\).
The minor axis is the shortest diameter of the ellipse, with length \(2b\).
The foci are two fixed points inside the ellipse that define its shape.
Based on these properties, the equation for the distance from a point \((x, y)\) on the ellipse to one of the foci \((c, 0)\) is:
\[
\sqrt{(x – c)^2 + y^2} + \sqrt{(x + c)^2 + y^2} = 2a
\]
Simplify and solve for \(y^2\):
\[
y^2 = a^2 \left(1 – \frac{x^2}{c^2}\right)
\]
Using the Pythagorean theorem \(a^2 = b^2 + c^2\), substitute \(c^2 = a^2 – b^2\):
\[
y^2 = \frac{a^2 b^2}{a^2 – b^2} – \frac{b^2 x^2}{a^2 – b^2}
\]
Multiply both sides by \(a^2 – b^2\) to eliminate the denominators:
\[
(a^2 – b^2)y^2 = a^2 b^2 – b^2 x^2
\]
Substitute \(a^2 – b^2\) with \(c\) and rearrange the terms:
\[
c^2 y^2 + b^2 x^2 = a^2 b^2
\]
Divide both sides by \(a^2 b^2\) to obtain the standard form equation:
\[
\frac{x^2}{a^2} + \frac{y^2}{b^2} = \frac{c^2}{a^2 b^2} = 1
\]
This is the general equation of an ellipse with the center at the origin. If the center is not at the origin \((h, k)\), apply a translation by substituting \(x – h\) for \(x\) and \(y – k\) for \(y\):
\[
\frac{{(x – h)^2}}{{a^2}} + \frac{{(y – k)^2}}{{b^2}} = 1
\]
This equation represents an ellipse with center \((h, k)\), semi-major axis \(a\), and semi-minor axis \(b\).
Thanks for reading the post Equation of Ellipse Calculator.
Read: