The Equation of Hyperbola Calculator is a tool to get the equation of the Hyperbola if the user provides the required inputs.
Hyperbola Equation Generator
Equation of Hyperbola Calculator
\( \frac{(x – h)^2}{a^2} – \frac{(y – k)^2}{b^2} = 1 \)
\( \frac{(y – k)^2}{a^2} – \frac{(x – h)^2}{b^2} = 1 \)
where:
handkare the coordinates of the center of the hyperbolaais the length of the semi-major axis (the longer of the two axes)bis the length of the semi-minor axis
In both equations, the constant on the right side of the equation is 1. This can be changed to any other positive constant, but it will not affect the shape of the hyperbola.
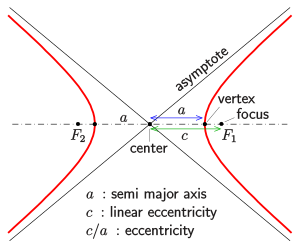
To find the equation of a hyperbola, you need to know the center, the semi-major axis, and the semi-minor axis. Once you have these values, you can plug them into the appropriate standard equation.
For example, let’s say the center of the hyperbola is (2, 3), the semi-major axis is 5, and the semi-minor axis is 4. The equation of the hyperbola would be:
(x - 2)^2 / 25 - (y - 3)^2 / 16 = 1
This hyperbola would be centered at (2, 3), and it would have a horizontal width of 10 units and a vertical height of 8 units.
Properties of Hyperbolas
- The two branches of a hyperbola are always symmetrical about the center.
- The asymptotes of a hyperbola are lines that the branches approach as they get further away from the center.
- The distance between a point on the hyperbola and a focus is always the same.
Read: