Natural Log Calculator is a tool to calculate the Natural Log of a number. The user will input the number and the Log of the number will be given.
Natural Logarithm Calculator
The logarithm of a number is a mathematical operation that measures the exponent to which a specified base must be raised to obtain that number. In simpler terms, the logarithm helps us find out how many times we need to multiply the base by itself to get the desired number. Logarithms are used to solve equations involving exponential growth or decay, as well as to simplify complex calculations involving very large or very small numbers.
The notation for the logarithm of a number \(x\) to the base \(b\) is commonly written as \(\log_b(x)\). Here, \(b\) is the base, \(x\) is the number whose logarithm we want to find, and the result of \(\log_b(x)\) is the exponent to which \(b\) must be raised to equal \(x\).
Key points to understand about logarithms:
1. Logarithmic and Exponential Relationships:
Logarithms and exponentials are inverse operations. If \(y = b^x\), then \(\log_b(y) = x\). In other words, taking the logarithm “undoes” the exponentiation operation, and vice versa.
2. Properties of Logarithms:
Logarithms have several important properties that make them useful in solving various mathematical problems. For example:
– \(\log_b(1) = 0\): The logarithm of 1 to any base is always 0.
– \(\log_b(b) = 1\): The logarithm of the base itself is always 1.
– \(\log_b(a \cdot c) = \log_b(a) + \log_b(c)\): The logarithm of a product is the sum of the logarithms.
– \(\log_b\left(\frac{a}{c}\right) = \log_b(a) – \log_b(c)\): The logarithm of a quotient is the difference of the logarithms.
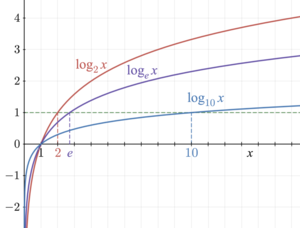
3. Common Bases:
While logarithms can have any positive base, certain bases are more commonly used:
– Common Logarithm (\(\log_{10}(x)\)): Logarithm to the base 10. It’s used in applications involving powers of 10, such as orders of magnitude and decimal calculations.
– Natural Logarithm (\(\ln(x)\)): Logarithm to the base \(e\), Euler’s number (approximately 2.71828). It’s frequently used in calculus, particularly in exponential growth and decay.
4. Applications:
Logarithms have wide-ranging applications, including in science, engineering, finance, computer science, and more. They help solve problems involving exponential growth, interest calculations, population growth, and signal processing, among others.
Thanks for reading the post Natural Log Calculator.
Read: