The Phase and Magnitude Calculator is a tool to calculate the magnitude and phase of the vector. In vector mathematics, a vector is represented in terms of its phase (angle) and magnitude (length). These two properties help describe the direction and size of the vector, respectively.
Vector Magnitude and Phase
| Vector Components (Vx, Vy) | Magnitude (|V|) | Phase (θ) | |
|---|---|---|---|
Let us explore each concept:
- Magnitude (Length):
- The magnitude of a vector, denoted as |V| or simply V, represents the length or size of the vector.
- It is always a non-negative value and can be thought of as the “strength” or “quantity” of the vector.
- The magnitude is a scalar quantity, meaning it has no direction. It’s just a numerical value.
- In physics, magnitude is often used to represent physical quantities like speed, force, and distance. For example, if you have a vector representing the velocity of an object, its magnitude would indicate its speed.
- Phase (Angle):
- The phase of a vector, often denoted as θ (theta), represents the direction in which the vector is pointing in relation to some reference direction (usually an axis).
- It is measured in degrees or radians, depending on the context.
- The phase gives information about the orientation of the vector in a coordinate system. For instance, in a two-dimensional Cartesian coordinate system, the phase represents the angle between the vector and the positive x-axis.
- Unlike magnitude, the phase is a directional quantity. It provides information about where the vector points in space.
To visualize this, consider a vector in a two-dimensional plane (e.g., on a piece of paper). The magnitude of the vector is its length, and the phase is the angle it makes with respect to the positive x-axis.
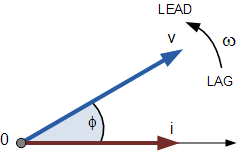
In polar coordinates, the vector can be represented as (r, θ), where ‘r’ is the magnitude, and ‘θ’ is the phase. In Cartesian coordinates, you can use the components of the vector (e.g., Vx and Vy) to find its magnitude and phase.
Magnitude Calculation
Mathematically, the magnitude (length) of a vector \( \mathbf{V} \) in two-dimensional Cartesian coordinates is represented as:
\[ |\mathbf{V}| = \sqrt{V_x^2 + V_y^2} \]
Where:
- \( |\mathbf{V}| \) is the magnitude of vector \( \mathbf{V} \).
- \( V_x \) is the x-component of vector \( \mathbf{V} \).
- \( V_y \) is the y-component of vector \( \mathbf{V} \).
In three-dimensional space, you would extend this concept by adding the z-component:
\[ |\mathbf{V}| = \sqrt{V_x^2 + V_y^2 + V_z^2} \]
Phase (Angle) Calculation
Mathematically, the phase (angle) of a vector \( \mathbf{V} \) in two-dimensional Cartesian coordinates is represented as an angle \( \theta \) with respect to the positive x-axis:
\[ \theta = \arctan\left(\frac{V_y}{V_x}\right) \]
Where:
- \( \theta \) is the phase (angle) of vector \( \mathbf{V} \).
- \( \arctan() \) is the inverse tangent function.
- \( V_y \) is the y-component of vector \( \mathbf{V} \).
- \( V_x \) is the x-component of vector \( \mathbf{V} \).
In three-dimensional space, finding the phase can be more complex, involving spherical or cylindrical coordinates, depending on the coordinate system being used. Thanks for reading the post Phase and Magnitude Calculator.